
Le 15 octobre 1586 débuta le procès pour trahison envers la reine Elizabeth d’Angleterre de Marie Stuart, reine d’Écosse. Sir Francis Walsingham, premier secrétaire de la reine Elizabeth et directeur du chiffre des services secrets, instruit l’accusation. Il doit prouver à sa reine la culpabilité de sa cousine pour que le procès se termine par une exécution. Exécution qui serait une première dans la politique de l’époque. Dans le cas d’une réussite de sa part, un monarque exécutant un autre ferait jurisprudence.
Marie Stuart était au courant de la conspiration que son plus fervent partisan. Sir Anthony Babington fomentait l’assassinat d’Elizabeth alors que sa reine était enfermée sous bonne garde. De par ses connexions, et grâce à un agent double, Walsingham envoyait des copies des lettres cryptées à Thomas Phelippes, le meilleur cryptanalyste d’Europe. Il eut donc les preuves pour confondre Marie. Et le 8 février 1587, Marie Stuart fut décapitée suite à sa culpabilité mis au jour.
Cet événement fit gronder tous les services secrets du monde. Et une méthode inviolable avait été mise au point en 1586 par Blaise de Vigenère. La même année où Thomas Phelippes avait brisé le code de Marie Stuart.
Chiffre Polyalphabétique
Comme nous l’avons vu, avec le précédent article, le chiffre monoalphabétique n’est plus sécurisé. Même utiliser une phrase clé n’empêche pas les cryptanalystes de casser le chiffre par la méthode des fréquences. C’est Léon Battista Alberti qui, vers 1460, lança les bases du chiffrement par plusieurs alphabets. Le principe est simple : la première lettre du message est chiffré avec le premier alphabet, la seconde lettre avec le second alphabet, le premier alphabet est réutilisé pour la troisième lettre, et ainsi de suite.
Exemple 1. Alphabet ordinaire : abcdefghijklmnopqrstuvwxyz Alphabet chiffré 1 : EPJFVIRKDSTLMNAUOQBGWHXYZC Alphabet chiffré 2 : TJGHWLQZSKBNDCIMOVREPUFAYX Message : Ce message est codé mais non caché Chiffré : JW MWBREQV WBE JIFW MTDR NIN GEGKW
Avec ce système de chiffrement, il est plus difficile d’utiliser la fréquence de lettre, car le e peut être chiffré en V ou W, qui eux-mêmes peuvent être le résultat du chiffrement respectifs de r ou u – en plus de e.
Ces travaux sont repris par l’abbé allemand Jean Trithème né en 1462, puis le savant italien Giovani Porta né en 1535, pour être mis en forme par le diplomate français Blaise de Vigenère.
Le Carré de Vigenère
L’idée est simple : Chaque lettre du message peut se voir chiffrée par n’importe quel alphabet de César. Seul un mot ou une phrase clé permet de connaître l’alphabet utilisé pour le chiffrer.
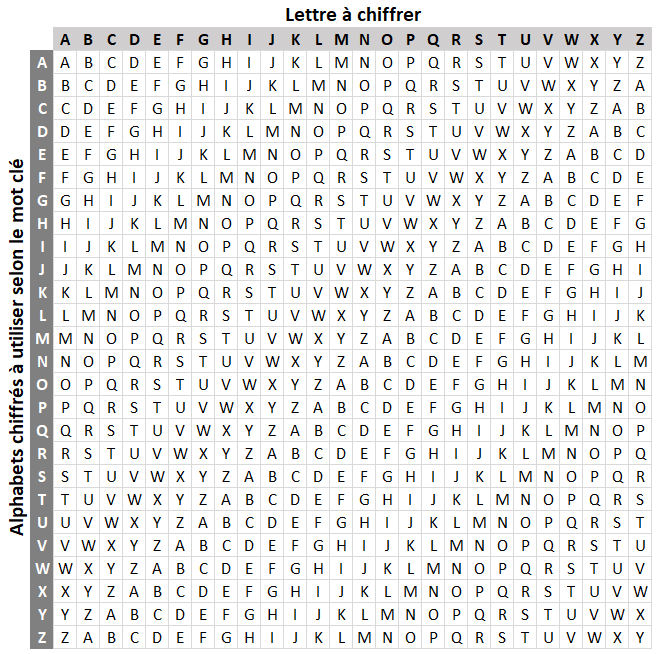
Exemple 2. Prenons le mot clé : VICTOIRE. Le message sera chiffré selon les lignes V, I, C, T, O, I, R, E et ainsi de suite. Chiffrons le mot Défaite : D => Ligne V => Y E => Ligne I => M F => Ligne C => H A => Ligne T => T I => Ligne O => W T => Ligne I => B E => Ligne R => V Message chiffré : YMHTWBV

Le plus grand atout de cette méthode vient du faite qu’une lettre double – comme le ll de ville – ne sera pas chiffré par la même lettre. Dans notre exemple ville devient QQNES.
Le plus gros désavantage, et la raison pour laquelle les secrétaires du chiffre européens ne l’ont pas utilisés, vient de la difficulté et du temps qu’il faut pour chiffrer et déchiffrer de longs messages avec cette méthode.
Substitution homophonique
Une solution plus pratique est l’utilisation de plusieurs symbole pour chiffrer la même lettre. Le plus remarquable est la substitution homophonique par les fréquences. Dans le cas du a – représentant 9% dans les textes français – on peut lui attribuer 9 symboles. Ces symboles seront utiliser aléatoirement et ne peuvent plus être identifier par l’analyse fréquentielle.
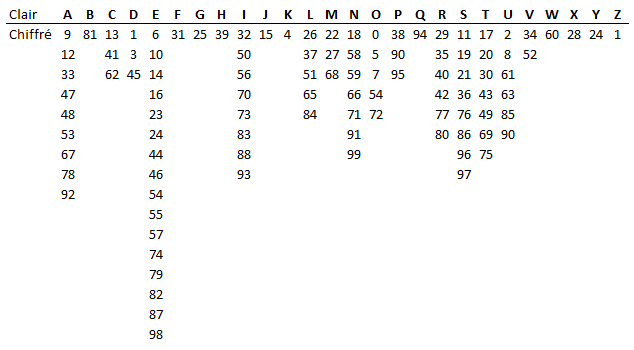
Exemple 3. Avec le tableau ci-dessus, chiffrons le message : CACHONS NOS SECRETS Chiffre 1 : 41 78 13 39 7 66 86 18 0 97 19 34 62 40 6 75 11 Chiffre 2 : 62 12 41 39 54 18 97 91 72 11 36 10 13 77 98 17 96
Dans des deux chiffrements de l’exemple 3, le déchiffrement est simple. Il faut repérer la valeur dans la table et retranscrire la lettre correspondante. L’analyse fréquentielle d’un texte long empêche l’émergence des lettres fortes, car chaque symbole – ici nombre – représente 1% de la lettre à chiffrer. Pour d – ayant une fréquence de 3% en français – les symboles 1, 3 et 45 ont une fréquence de 1%.
Le carré de Vigenère incassable ?
La substitution homophonique semble être une bonne alternative au carré de Vigenère. Mais les cryptanalystes attentifs se rappellerons que chaque langues ont leurs spécificités avec des lettres ayant leur caractère propre.
Prenons l’exemple du q en français. Dans la grande majorité des cas, le q est suivi du u. Étant une lettre rare, on peut supposer que le q ne sera représenter que par un seul symbole, tandis que le u le sera pas 6 symboles. L’analyse fréquentielle des digrammes peut avoir raison de cette méthode.
Par la suite, nous pourrons voir comment la substitution est devenu une base pour le Grand Chiffre de Louis XIV, chiffre alimentant les rumeurs autour du Masque de Fer, mais aussi comment un anglais, considérer comme l’inventeur ayant établi le base de l’ordinateur moderne, réussi à déchiffrer l’indéchiffrable Carré de Vigenère en 1854.



